链表 链表结构定义 JAVA 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public class ListNode { int val; ListNode next; public ListNode () { } public ListNode (int val) { this .val = val; } public ListNode (int val, ListNode next) { this .val = val; this .next = next; } }
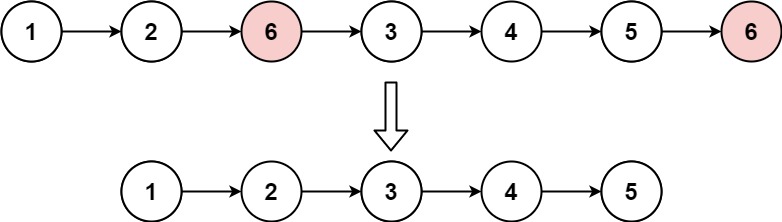
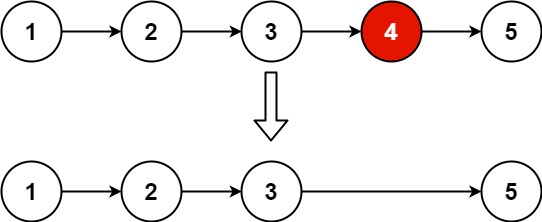
删除链表元素 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
示例 1:
1 2 输入:head = [1,2,6,3,4,5,6], val = 6 输出:[1,2,3,4,5]
示例 2:
1 2 输入:head = [], val = 1 输出:[]
示例 3:
1 2 输入:head = [7,7,7,7], val = 7 输出:[]
JAVA 不带头结点,但带pre结点 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class ListNode { int val; ListNode next; ListNode() {} ListNode(int val) { this .val = val; } ListNode(int val, ListNode next) { this .val = val; this .next = next; } } public class Solution203 { public static ListNode removeElements (ListNode head, int val) { while (head != null && head.val == val) { head = head.next; } if (head == null ) { return null ; } ListNode pre = head; ListNode cur = head.next; while (cur != null ) { if (cur.val == val) { pre.next = cur.next; } else { pre = cur; } cur = cur.next; } return head; } }
带虚拟头结点 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public ListNode removeElements (ListNode head, int val) { if (head == null ) { return head; } ListNode dummy = new ListNode (-1 , head); ListNode pre = dummy; ListNode cur = head; while (cur != null ) { if (cur.val == val) { pre.next = cur.next; } else { pre = cur; } cur = cur.next; } return dummy.next; }
不带虚拟头结点和pre结点 1 2 3 4 5 6 7 8 9 10 11 12 13 public ListNode removeElements (ListNode head, int val) { while (head!=null && head.val==val){ head = head.next; } ListNode curr = head; while (curr!=null ){ while (curr.next!=null && curr.next.val == val){ curr.next = curr.next.next; } curr = curr.next; } return head; }
设计链表 你可以选择使用单链表或者双链表,设计并实现自己的链表。
单链表中的节点应该具备两个属性:val 和 next 。val 是当前节点的值,next 是指向下一个节点的指针/引用。
如果是双向链表,则还需要属性 prev 以指示链表中的上一个节点。假设链表中的所有节点下标从 0 开始。
实现 MyLinkedList 类:
MyLinkedList() 初始化 MyLinkedList 对象。int get(int index) 获取链表中下标为 index 的节点的值。如果下标无效,则返回 -1 。void addAtHead(int val) 将一个值为 val 的节点插入到链表中第一个元素之前。在插入完成后,新节点会成为链表的第一个节点。void addAtTail(int val) 将一个值为 val 的节点追加到链表中作为链表的最后一个元素。void addAtIndex(int index, int val) 将一个值为 val 的节点插入到链表中下标为 index 的节点之前。如果 index 等于链表的长度,那么该节点会被追加到链表的末尾。如果 index 比长度更大,该节点将 不会插入 到链表中。void deleteAtIndex(int index) 如果下标有效,则删除链表中下标为 index 的节点。
示例:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 输入 ["MyLinkedList", "addAtHead", "addAtTail", "addAtIndex", "get", "deleteAtIndex", "get"] [[], [1], [3], [1, 2], [1], [1], [1]] 输出 [null, null, null, null, 2, null, 3] 解释 MyLinkedList myLinkedList = new MyLinkedList(); myLinkedList.addAtHead(1); myLinkedList.addAtTail(3); myLinkedList.addAtIndex(1, 2); // 链表变为 1->2->3 myLinkedList.get(1); // 返回 2 myLinkedList.deleteAtIndex(1); // 现在,链表变为 1->3 myLinkedList.get(1); // 返回 3
代码 单链表 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 public class ListNode { int val; ListNode next; ListNode() {} ListNode(int val) { this .val = val; } ListNode(int val, ListNode next) { this .val = val; this .next = next; } } class MyLinkedList { int size; ListNode head; public MyLinkedList () { this .size = 0 ; this .head = new ListNode (0 ); } public int get (int index) { if (index < 0 || this .size <= index) { return -1 ; } else { ListNode cur = head; for (int i = 0 ; i <= index; i++) { cur = cur.next; } return cur.val; } } public void addAtHead (int val) { addAtIndex(0 ,val); } public void addAtTail (int val) { addAtIndex(size,val); } public void addAtIndex (int index, int val) { if (index > size){ return ; } if (index < 0 ){ index = 0 ; } ListNode cur = new ListNode (val); ListNode pre = head; for (int i = 0 ;i < index;i++) { pre = pre.next; } cur.next = pre.next; pre.next = cur; size++; } public void deleteAtIndex (int index) { if (size > index) { ListNode pre = head; if (index == 0 ) { head.next = head.next.next; size--; return ; } for (int i = 0 ; i < index; i++) { pre = pre.next; } pre.next = pre.next.next; size--; } } }
双链表 翻转链表 双指针法 首先定义一个cur指针,指向头结点,再定义一个pre指针,初始化为null。
然后就要开始反转了,首先要把 cur->next 节点用tmp指针保存一下,也就是保存一下这个节点。
为什么要保存一下这个节点呢,因为接下来要改变 cur->next 的指向了,将cur->next 指向pre ,此时已经反转了第一个节点了。
接下来,就是循环走如下代码逻辑了,继续移动pre和cur指针。
最后,cur 指针已经指向了null,循环结束,链表也反转完毕了。 此时我们return pre指针就可以了,pre指针就指向了新的头结点。
提示:这个图是错的,应该先移动pre到cur所指的位置,然后再移动cur
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution { public ListNode reverseList (ListNode head) { ListNode pre = null ; ListNode cur = head; ListNode tmp = null ; while (cur != null ) { tmp = cur.next; cur.next = pre; pre = cur; cur = tmp; } return pre; } }
递归法 其实递归要对应这双指针才能看得懂,return reverse(null, head);是因为我们在双指针中赋值的时候就是让cur = head,tmp = null
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution { public ListNode reverseList (ListNode head) { return reverse(null , head); } private ListNode reverse (ListNode prev, ListNode cur) { if (cur == null ) { return prev; } ListNode temp = null ; temp = cur.next; cur.next = prev; return reverse(cur, temp); } }
从后往前递归 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution { ListNode reverseList (ListNode head) { if (head == null ) return null ; if (head.next == null ) return head; ListNode last = reverseList(head.next); head.next.next = head; head.next = null ; return last; } }
使用虚拟头结点解决链表翻转 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public static ListNode reverseList1 (ListNode head) { ListNode dumpyHead = new ListNode (-1 ); dumpyHead.next = null ; ListNode cur = head; while (cur != null ){ ListNode temp = cur.next; cur.next = dumpyHead.next; dumpyHead.next = cur; cur = temp; } return dumpyHead.next; }
两两交换链表中的节点 给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
示例 1:
1 2 输入:head = [1,2,3,4] 输出:[2,1,4,3]
示例 2:
示例 3:
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public static ListNode swapPairs (ListNode head) { ListNode dummyhead = new ListNode (-1 ); dummyhead.next = head; ListNode cur = dummyhead; ListNode tmp; ListNode first; ListNode second; while (cur.next != null && cur.next.next != null ) { tmp = cur.next.next.next; first = cur.next; second = cur.next.next; cur.next = second; second.next = first; first.next = tmp; cur = first; } return dummyhead.next; }
流程图 刚开始
之后
删除链表的倒数第N个节点 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
示例 1:
1 2 输入:head = [1,2,3,4,5], n = 2 输出:[1,2,3,5]
示例 2:
1 2 输入:head = [1], n = 1 输出:[]
示例 3:
1 2 输入:head = [1,2], n = 1 输出:[1]
分析 这道题不一般之处在于,强调要删除链表的倒数第N个节点,那么很多人的第一个想法是先数数一共有几个节点,然后再去移动指针。但是使用快慢指针就能解决这个问题,且不需要计算节点个数。
那么如何使用呢?首先思考一下倒数第N个,我们知道最后一个节点一定是空节点,那么这个N相当于要删除节点和空节点有N个距离。那么我们先让快慢指针同时指向头结点,然后再让快指针先移动N+1步,则此时快慢指针之间距离为N+1。
我们再让快指针和慢指针同时移动,则他们的距离始终保持,当快指针指向空节点的时候,慢指针正好指向要删除节点的前一个节点,那么删除就很容易了。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public static ListNode removeNthFromEnd (ListNode head, int n) { ListNode dummyhead = new ListNode (-1 ); dummyhead.next = head; ListNode fast = dummyhead; ListNode slow = dummyhead; for (int i = 1 ; i <= n + 1 ; i++){ fast = fast.next; } while (fast != null ) { fast = fast.next; slow = slow.next; } slow.next = slow.next.next; return dummyhead.next; }
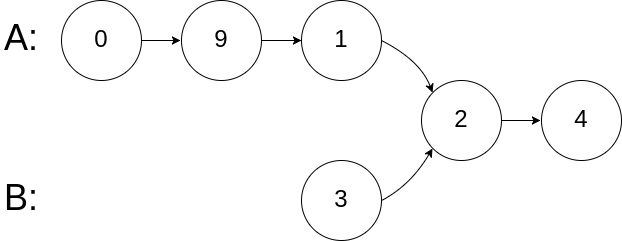
链表相交 给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点,返回 null 。
图示两个链表在节点 c1 开始相交:
题目数据 保证 整个链式结构中不存在环。
注意 ,函数返回结果后,链表必须 保持其原始结构 。
示例 1:
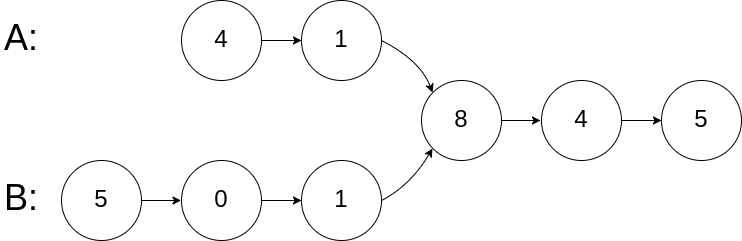
1 2 3 4 5 输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3 输出:Intersected at '8' 解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。 从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。 在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
示例 2:
1 2 3 4 5 输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1 输出:Intersected at '2' 解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。 从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。 在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
1 2 3 4 5 输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2 输出:null 解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。 由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。 这两个链表不相交,因此返回 null 。
分析 为什么不能好好说人话呢?云里雾里!
看看英文题目吧。
Given two (singly) linked lists, determine if the two lists intersect. Return the inter secting node. Note that the intersection is defined based on reference(引用), not value(值). That is, if the kth node of the first linked list is the exact same node (by reference) as the jth node of the second linked list, then they are intersecting.
简单来说,就是求两个链表交点节点的指针 。 交点不是数值相等,而是指针相等。
为了方便举例,假设节点元素数值相等,则节点指针相等。
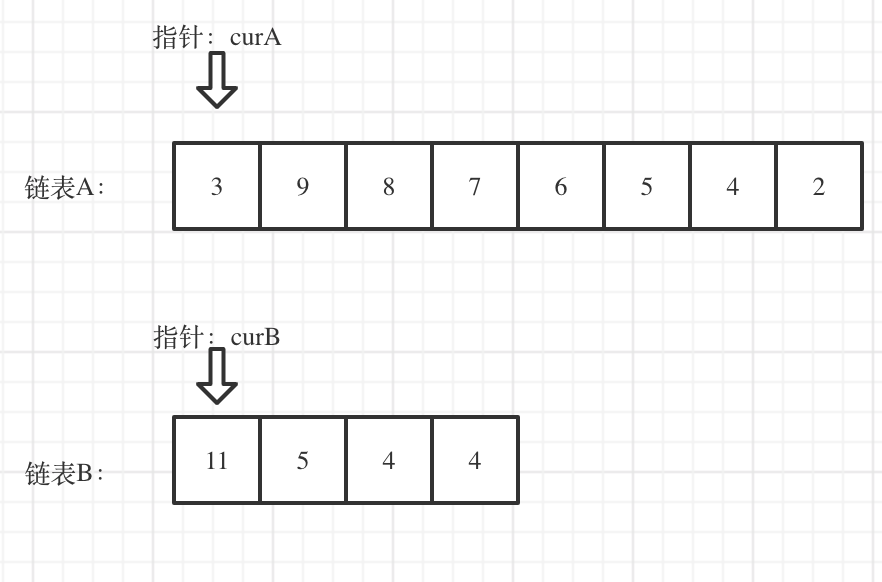
看如下两个链表,目前curA指向链表A的头结点,curB指向链表B的头结点:
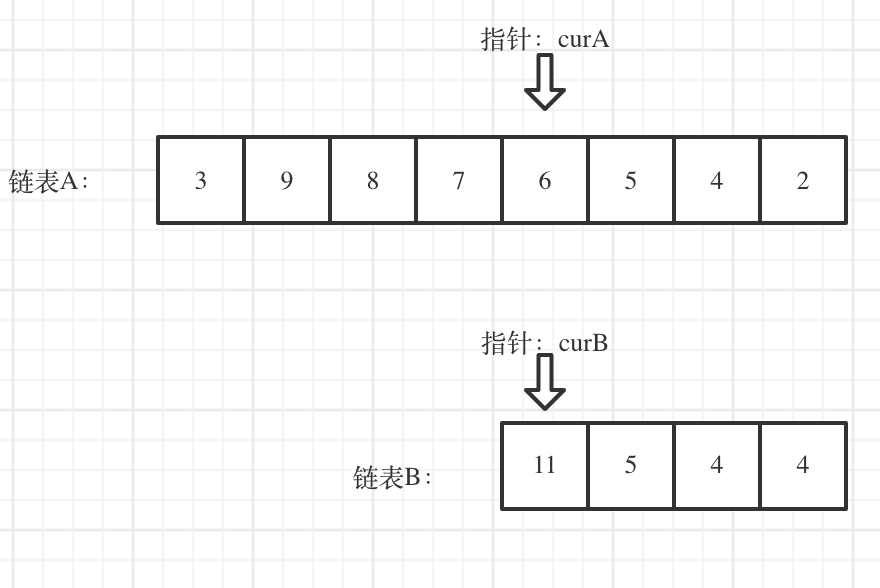
我们求出两个链表的长度,并求出两个链表长度的差值,然后让curA移动到,和curB 末尾对齐的位置,如图:
此时我们就可以比较curA和curB是否相同,如果不相同,同时向后移动curA和curB,如果遇到curA == curB,则找到焦点。
否则循环退出返回空指针。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 ListNode cura = headA;ListNode curb = headB;int lena = 0 ;int lenb = 0 ;while (cura != null ) { cura = cura.next; lena++; } while (curb != null ) { curb = curb.next; lenb++; } cura = headA; curb = headB; if (lenb > lena) { int t = lenb; lenb = lena; lena = t; ListNode tmp = curb; curb = cura; cura = tmp; } int len = lena - lenb;while (len-- > 0 ) { cura = cura.next; } while (cura != null ) { if (cura == curb) { return cura; }else { cura = cura.next; curb = curb.next; } } return null ;
总结 我好像明白了这里所说的基于引用而不是基于值是什么意思。
很多人对这个样例有疑问,他们质疑为什么交点不是1呢,那是因为这个链表真实的物理地址就如图所示,他们共同指向了同一个数据域为8的节点,而他们都有一个数据域为1的节点,但这两个节点的地址可不一样。
环形链表 给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始 )。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递 ,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:
1 2 3 输入:head = [3,2,0,-4], pos = 1 输出:返回索引为 1 的链表节点 解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
1 2 3 输入:head = [1,2], pos = 0 输出:返回索引为 0 的链表节点 解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
1 2 3 输入:head = [1], pos = -1 输出:返回 null 解释:链表中没有环。
分析
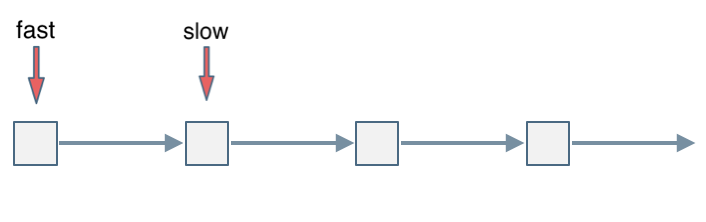
判断链表是否有环
可以使用快慢指针法,分别定义 fast 和 slow 指针,从头结点出发,fast指针每次移动两个节点,slow指针每次移动一个节点,如果 fast 和 slow指针在途中相遇 ,说明这个链表有环。
为什么fast 走两个节点,slow走一个节点,有环的话,一定会在环内相遇呢,而不是永远的错开呢
首先第一点:fast指针一定先进入环中,如果fast指针和slow指针相遇的话,一定是在环中相遇,这是毋庸置疑的。
那么来看一下,为什么fast指针和slow指针一定会相遇呢?
可以画一个环,然后让 fast指针在任意一个节点开始追赶slow指针。
会发现最终都是这种情况, 如下图:
fast和slow各自再走一步, fast和slow就相遇了
这是因为fast是走两步,slow是走一步,其实相对于slow来说,fast是一个节点一个节点的靠近slow的 ,所以fast一定可以和slow重合。
动画如下:
如果有环,如何找到这个环的入口
此时已经可以判断链表是否有环了,那么接下来要找这个环的入口了。
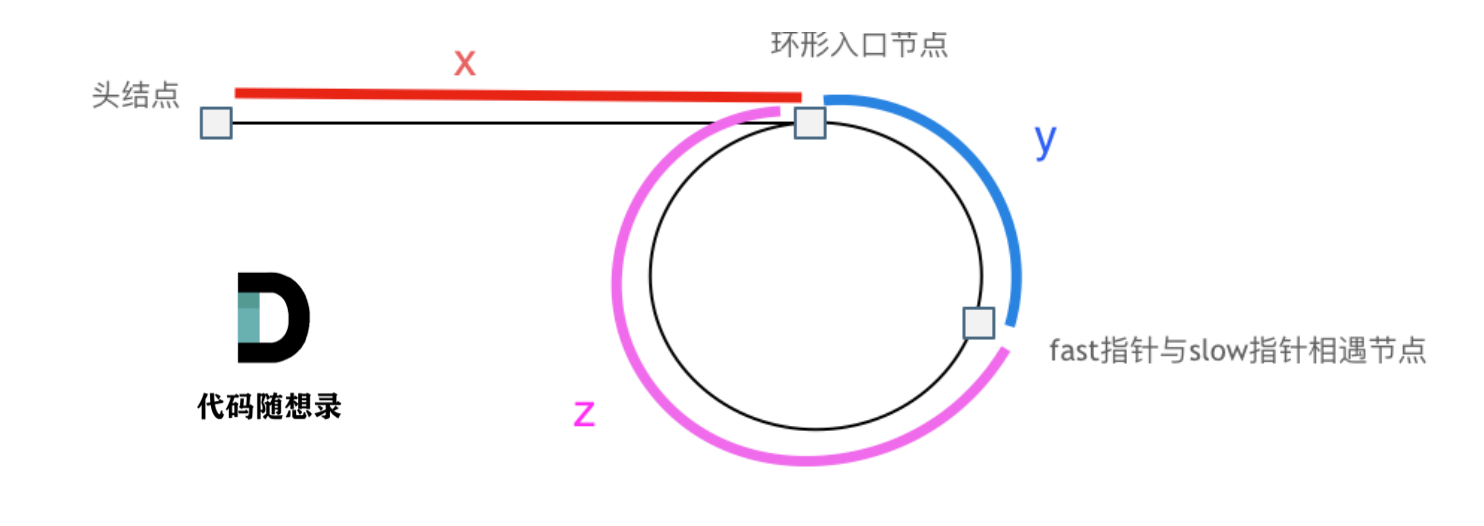
假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点 节点数为y。 从相遇节点 再到环形入口节点节点数为 z。 如图所示:
那么相遇时: slow指针走过的节点数为: x + y, fast指针走过的节点数:x + y + n (y + z),n为fast指针在环内走了n圈才遇到slow指针, (y+z)为 一圈内节点的个数A。
因为fast指针是一步走两个节点,slow指针一步走一个节点, 所以 fast指针走过的节点数 = slow指针走过的节点数 * 2:
1 (x + y) * 2 = x + y + n (y + z)
两边消掉一个(x+y): x + y = n (y + z)
因为要找环形的入口,那么要求的是x,因为x表示 头结点到 环形入口节点的的距离。
所以要求x ,将x单独放在左面:x = n (y + z) - y ,
再从n(y+z)中提出一个 (y+z)来,整理公式之后为如下公式:x = (n - 1) (y + z) + z 注意这里n一定是大于等于1的,因为 fast指针至少要多走一圈才能相遇slow指针。
这个公式说明什么呢?
先拿n为1的情况来举例,意味着fast指针在环形里转了一圈之后,就遇到了 slow指针了。
当 n为1的时候,公式就化解为 x = z,
这就意味着,从头结点出发一个指针,从相遇节点 也出发一个指针,这两个指针每次只走一个节点, 那么当这两个指针相遇的时候就是 环形入口的节点 。
也就是在相遇节点处,定义一个指针index1,在头结点处定一个指针index2。
让index1和index2同时移动,每次移动一个节点, 那么他们相遇的地方就是 环形入口的节点。
动画如下:
那么 n如果大于1是什么情况呢,就是fast指针在环形转n圈之后才遇到 slow指针。
其实这种情况和n为1的时候 效果是一样的,一样可以通过这个方法找到 环形的入口节点,只不过,index1 指针在环里 多转了(n-1)圈,然后再遇到index2,相遇点依然是环形的入口节点。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 ListNode fast = head;ListNode slow = head;while (fast != null && fast.next != null ){ fast = fast.next.next; slow = slow.next; if (fast == slow) { ListNode index1 = head; ListNode index2 = fast; while (index1 != index2) { index1 = index1.next; index2 = index2.next; } return index2; } } return null ;
总结