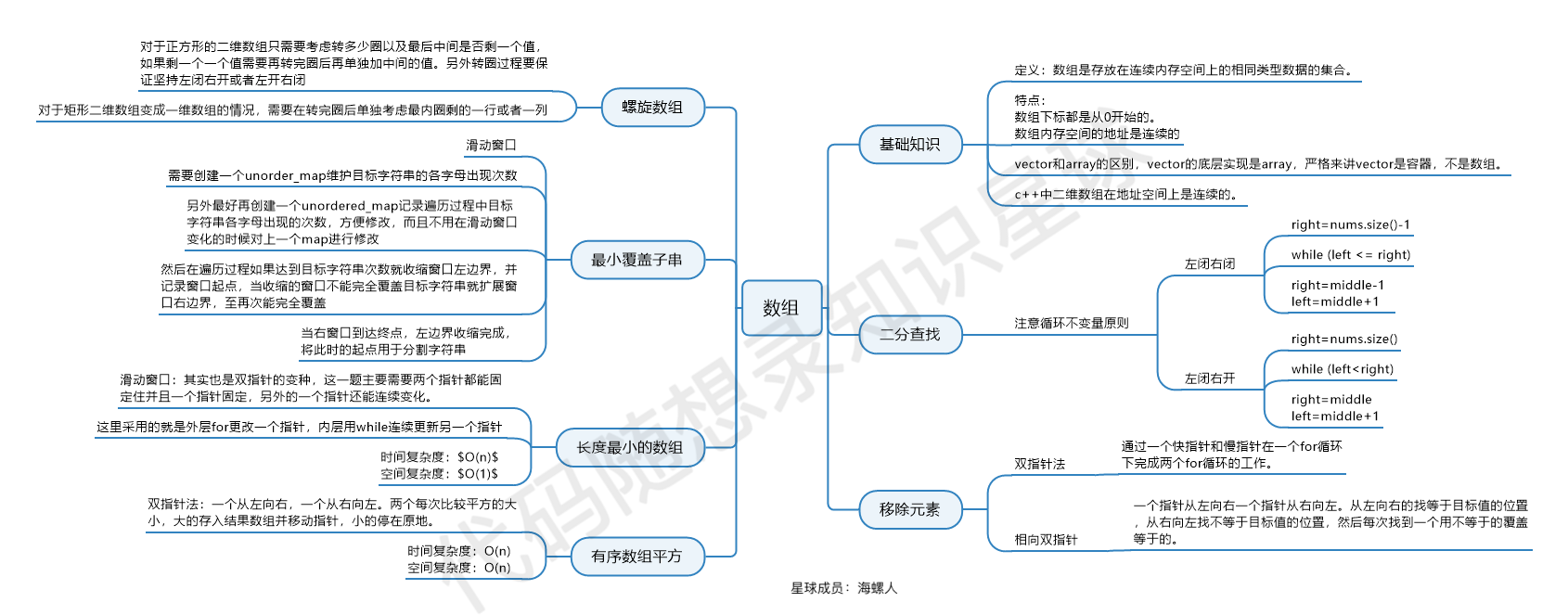
数组

查找

二分查找

C

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// (版本一) 左闭右闭区间 [left, right]
int search(int* nums, int numsSize, int target){
    int left = 0;
    int right = numsSize-1;
    int middle = 0;
    //若left小于等于right，说明区间中元素不为0
    while(left<=right) {
        //更新查找下标middle的值
        middle = (left+right)/2;
        //此时target可能会在[left,middle-1]区间中
        if(nums[middle] > target) {
            right = middle-1;
        } 
        //此时target可能会在[middle+1,right]区间中
        else if(nums[middle] < target) {
            left = middle+1;
        } 
        //当前下标元素等于target值时，返回middle
        else if(nums[middle] == target){
            return middle;
        }
    }
    //若未找到target元素，返回-1
    return -1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// (版本二) 左闭右开区间 [left, right)
int search(int* nums, int numsSize, int target){
    int length = numsSize;
    int left = 0;
    int right = length;	//定义target在左闭右开的区间里，即：[left, right)
    int middle = 0;
    while(left < right){  // left == right时，区间[left, right)属于空集，所以用 < 避免该情况
        int middle = left + (right - left) / 2;
        if(nums[middle] < target){
            //target位于(middle , right) 中为保证集合区间的左闭右开性，可等价为[middle + 1,right)
            left = middle + 1;
        }else if(nums[middle] > target){
            //target位于[left, middle)中
            right = middle ;
        }else{	// nums[middle] == target ，找到目标值target
            return middle;
        }
    }
    //未找到目标值，返回-1
    return -1;
}

JAVA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int search(int[] nums, int target) {
        // 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算
        if (target < nums[0] || target > nums[nums.length - 1]) {
            return -1;
        }
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            if (nums[mid] == target)
                return mid;
            else if (nums[mid] < target)
                left = mid + 1;
            else if (nums[mid] > target)
                right = mid - 1;
        }
        return -1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int search(int[] nums, int target) {
        int left = 0, right = nums.length;
        while (left < right) {
            int mid = left + ((right - left) >> 1);
            if (nums[mid] == target)
                return mid;
            else if (nums[mid] < target)
                left = mid + 1;
            else if (nums[mid] > target)
                right = mid;
        }
        return -1;
    }
}

python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1  # 定义target在左闭右闭的区间里，[left, right]

        while left <= right:
            middle = left + (right - left) // 2
            
            if nums[middle] > target:
                right = middle - 1  # target在左区间，所以[left, middle - 1]
            elif nums[middle] < target:
                left = middle + 1  # target在右区间，所以[middle + 1, right]
            else:
                return middle  # 数组中找到目标值，直接返回下标
        return -1  # 未找到目标值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums)  # 定义target在左闭右开的区间里，即：[left, right)

        while left < right:  # 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
            middle = left + (right - left) // 2

            if nums[middle] > target:
                right = middle  # target 在左区间，在[left, middle)中
            elif nums[middle] < target:
                left = middle + 1  # target 在右区间，在[middle + 1, right)中
            else:
                return middle  # 数组中找到目标值，直接返回下标
        return -1  # 未找到目标值

移除元素

暴力方法

JAVA

1

双指针法

JAVA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//没有改变元素相对位置
class Solution {
    public int removeElement(int[] nums, int val) {
        // 快慢指针
        int slowIndex = 0;
        for (int fastIndex = 0; fastIndex < nums.length; fastIndex++) {
            if (nums[fastIndex] != val) {
                nums[slowIndex] = nums[fastIndex];
                slowIndex++;
            }
        }
        return slowIndex;
        // slowIndex为移除元素后的数组元素个数
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//相向双指针法
//改变了元素相对位置，确保了移动最少元素
class Solution {
    public int removeElement(int[] nums, int val) {
        int left = 0;
        int right = nums.length - 1;
        while(right >= 0 && nums[right] == val) right--; //将right移到从右数第一个值不为val的位置
        while(left <= right) {
            if(nums[left] == val) { //left位置的元素需要移除
                //将right位置的元素移到left（覆盖），right位置移除
                nums[left] = nums[right];
                right--;
            }
            left++;
            while(right >= 0 && nums[right] == val) right--;
        }
        return left;
    }
}

长度最小的子数组

暴力方法

滑动窗口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {

    // 滑动窗口
    public int minSubArrayLen(int s, int[] nums) {
        int left = 0;//滑动窗口的起始位置
        int sum = 0;//滑动窗口数值之和
        int result = Integer.MAX_VALUE;//滑动窗口的长度
        for (int right = 0; right < nums.length; right++) {
            sum += nums[right];
            while (sum >= s) {
                result = Math.min(result, right - left + 1);
                sum -= nums[left++];//不断变更起始位置
            }
        }
        return result == Integer.MAX_VALUE ? 0 : result;//如果result没有被赋值就返回0，说明没有找到符合条件的子序列
    }
}

相关题目

904 水果成篮

你正在探访一家农场，农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示，其中 fruits[i] 是第 i 棵树上的水果 种类 。

你想要尽可能多地收集水果。然而，农场的主人设定了一些严格的规矩，你必须按照要求采摘水果：

  • 你只有 两个 篮子，并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
  • 你可以选择任意一棵树开始采摘，你必须从 每棵 树（包括开始采摘的树）上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次，你将会向右移动到下一棵树，并继续采摘。
  • 一旦你走到某棵树前，但水果不符合篮子的水果类型，那么就必须停止采摘。

给你一个整数数组 fruits ，返回你可以收集的水果的 最大 数目。

示例 1：

1
2
3
输入：fruits = [1,2,1]
输出：3
解释：可以采摘全部 3 棵树。

示例 2：

1
2
3
4
输入：fruits = [0,1,2,2]
输出：3
解释：可以采摘 [1,2,2] 这三棵树。
如果从第一棵树开始采摘，则只能采摘 [0,1] 这两棵树。

示例 3：

1
2
3
4
输入：fruits = [1,2,3,2,2]
输出：4
解释：可以采摘 [2,3,2,2] 这四棵树。
如果从第一棵树开始采摘，则只能采摘 [1,2] 这两棵树。

示例 4：

1
2
3
输入：fruits = [3,3,3,1,2,1,1,2,3,3,4]
输出：5
解释：可以采摘 [1,2,1,1,2] 这五棵树。
分析

该题就是要寻找子序列，但是题干写的很抽象，用人话就是说要寻找最多只包含两种元素的最长子串，然后返回长度。为什么只能有两种元素呢，因为题目描述里面说只有两个篮子。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public int totalFruit(int[] fruits) {
        int left = 0;//滑动窗口的起始位置
        int right = 0;//滑动窗口的终止位置
        int result = 0;//滑动窗口的长度
        int l = fruits[left];//第一个篮子
        int r = fruits[right];//第二个篮子
        while(right < fruits.length)
        {
            if(fruits[right] == l || fruits[right] == r)//遇到的元素仍是篮子里装的两种
            {
                result = Math.max(result,right - left + 1);//更新结果
                right++;//滑动窗口向右移动

            }
            else//此时遇到的元素不是篮子里的两种
            {
                left = right - 1;//此时right所在位置的果树是新元素（理解为第三种），那么right-1所在的位置就是第二个篮子里的元素，此时要抛弃掉第一个篮子里所装的元素
                l = fruits[left];//将第二个篮子里的元素装进第一个篮子里，
                while(left >= 1 && fruits[left - 1] == l)
                {
                    left--;//将第一个篮子慢慢回退齐所有的连续同类
                }
                r = fruits[right];//同时将新遇到的元素装入第二个篮子里
                result = Math.max(result,right - left + 1);//再次更新结果
            }
        }
        return result;//返回结果
    }
}

76 最小覆盖子串

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

  • 对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
  • 如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：

1
2
3
输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"
解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。

示例 2：

1
2
3
输入：s = "a", t = "a"
输出："a"
解释：整个字符串 s 是最小覆盖子串。

示例 3:

1
2
3
4
输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。
分析

76. 最小覆盖子串 - 力扣（Leetcode）

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
public static String minWindow(String s, String t) {
    if(s == null || s.length() == 0 || t == null || t.length() == 0)
    {
    	return "";
    }
    int l = 0;
    //滑动窗口的左边界
    int r = 0;
    //滑动窗口的有边界
    int[] need = new int [200];
    int size = Integer.MAX_VALUE;
    //子串长度
    int count = t.length();
    //t中字符的个数
    int start = 0;
    //最小串时的起始位置
    for(int i = 0;i < t.length();i++)
    {
        need[t.charAt(i)]++;
    }
    while(r < s.length())
    {
        char c = s.charAt(r);
        if(need[c] > 0)
        //此时遇到了所需的字符
        {
            count--;
        }
        need[c]--;
        //将该字符加入窗口中
        if(count == 0)
        /*此时窗口中已经覆盖了所有所需要的字符,应该不断增加l使得滑动窗口缩小，直到
        直到碰到一个必须包含的元素，这个时候不能再扔了，再扔就不满足条件了，
        记录此时滑动窗口的长度，并保存最小值
         */
        {
            while(true)
            {
                c = s.charAt(l);
                if(need[c] == 0)
                //此时表示遇到了必须包含的元素，所以退出该循环
                //为什么呢？因为t中的字符已经在need中赋过值，所以当count为0时
                //其在need中的数值早已为0，而其他无关字符的值为负数
                {
                    break;
                }
                need[c] += 1;
                //因为该元素不是所需的元素，被移出窗口，所以要将其对应的值加1
                l++;
                //此时没有遇到必须要包含的元素，因此要向右移动l

            }
            if(r - l + 1 < size)
            {
                size = r - l + 1;
                //更新长度
                start = l;
                //更新最小覆盖字串的起始位置
            }
            need[s.charAt(l)]++;
            //此时l所在位置的字符要被移出窗口，所以其对应的值加1
            l++;
            //将l增加一个位置，寻找新的满足条件的滑动窗口
            count++;
            //因为滑动窗口扔了一个必须包含的元素，所以要将count的值再加1
        }
        r++;
        //不断增加r使得滑动窗口增大，直到窗口中包含了t的所有元素
    }
    return size == Integer.MAX_VALUE ? "" : s.substring(start,start + size);
    //若size没有更新过，则证明没有找到该字串，应该返回空串，否则将返回最小覆盖字串
}

螺旋矩阵

相关题目

59 螺旋矩阵II

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
    public int[][] generateMatrix(int n) {
        int loop = 0;  // 控制循环次数
        int[][] res = new int[n][n];
        int start = 0;  // 每次循环的开始点(start, start)
        int count = 1;  // 定义填充数字
        int i, j;

        while (loop++ < n / 2) { // 判断边界后，loop从1开始
            // 模拟上侧从左到右
            for (j = start; j < n - loop; j++) {
                res[start][j] = count++;
            }

            // 模拟右侧从上到下
            for (i = start; i < n - loop; i++) {
                res[i][j] = count++;
            }

            // 模拟下侧从右到左
            for (; j >= loop; j--) {
                res[i][j] = count++;
            }

            // 模拟左侧从下到上
            for (; i >= loop; i--) {
                res[i][j] = count++;
            }
            start++;
        }

        if (n % 2 == 1) {
            res[start][start] = count;
        }

        return res;
    }
}

54 螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

img

1
2
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

img

1
2
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]
分析

与59.螺旋矩阵II不同的是：前题中的螺旋矩阵是正方形，只有正方形的边长n一个边界条件，而本题中，需要考虑长方形的长和宽(m行和n列)两个边界条件。自然，m可以等于n，即前题可视为本题在m==n的特殊情况。

我们从最一般的情况开始考虑，与59.螺旋矩阵II题解对比起来，m和n的带入，主要引来两方面的差异：

  • loop的计算： 本题的loop计算与59.螺旋矩阵II算法略微差异，因为存在rows和columns两个维度，可自行分析，loop只能取min(rows, columns)，例如rows = 5, columns = 7，那loop = 5 / 7 = 2
  • mid的计算及填充： 1、同样的原理，本题的mid计算也存在上述差异； 2、 如果min(rows, columns)为偶数，则不需要在最后单独考虑矩阵最中间位置的赋值 如果min(rows, columns)为奇数，则矩阵最中间位置不只是[mid][mid],而是会留下来一个特殊的中间行或者中间列，具体是中间行还是中间列，要看rows和columns的大小，如果rows > columns,则是中间列，相反，则是中间行
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
ArrayList<Integer> list = new ArrayList<>();
int rows = matrix.length;
int columns = matrix[0].length;
int i,j;
int startx = 0, starty = 0;
int loop = Math.min(rows, columns) / 2;
//循环的次数
int mid = loop;
int offset = 1;
//偏移量
while(loop > 0)
{
    for(j = starty;j < columns - offset;j++)
    {
        list.add(matrix[startx][j]);
    }
    for(i = startx;i < rows - offset;i++)
    {
        list.add(matrix[i][j]);
    }
    for(;j >= offset;j--)
    {
        list.add(matrix[i][j]);
    }
    for(;i >= offset;i--)
    {
        list.add(matrix[i][j]);
    }
    startx++;
    starty++;
    loop--;
    offset++;
}
if(Math.min(rows,columns) % 2 != 0)
{
    if(rows > columns)
    //行数大于列数，那么最后留下一列
    {
        for(i = mid;i <= mid + rows - columns;i++)
        {
            list.add(matrix[i][mid]);
        }
    }
    else
    //列数大于行数，则最后留下一行
    {
        for(j = mid;j <= mid + columns - rows;j++)
        {
            list.add(matrix[mid][j]);
        }
    }
}
return list;

29 顺时针打印矩阵

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。

示例 1：

1
2
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

1
2
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]
分析

该题目的矩阵行数和列数可以不相等，因此和54题大致是一样的，关键要处理剩下来的一行或一列

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
public int[] spiralOrder(int[][] matrix) {
    int rows = matrix.length;
    if(rows == 0)
    {
        return new int[0];
    }
    //若该矩阵为空，访问matrix[0]会出现错误，所以返回一个空矩阵
    int columns = matrix[0].length;
    int []ans = new int [rows * columns];
    int i,j;
    int count = 0;
    int startx = 0;
    int starty = 0;
    int loop = Math.min(rows,columns) / 2;
    int mid = loop;
    int offset = 1;
    while(loop > 0)
    {
        for(j = starty;j < columns - offset;j++)
        {
            ans[count] = matrix[startx][j];
            count++;
        }
        for(i = startx;i < rows - offset;i++)
        {
            ans[count] = matrix[i][j];
            count++;
        }
        for(;j >= offset;j--)
        {
            ans[count] = matrix[i][j];
            count++;
        }
        for(;i >= offset;i--)
        {
            ans[count] = matrix[i][j];
            count++;
        }
        startx++;
        starty++;
        offset++;
        loop--;
    }
    if(Math.min(rows,columns) % 2 != 0)
    {
        if(rows > columns)
        //行数大于列数，那么最后留下一列
        {
            for(i = mid;i <= mid + rows - columns;i++)
            {
                ans[count] = matrix[i][mid];
                count++;
            }
        }
        else
        //列数大于行数，则最后留下一行
        {
            for(j = mid;j <= mid + columns - rows;j++)
            {
                ans[count] = matrix[mid][j];
                count++;
            }
        }
    }
    return ans;

img